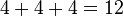เรียนคณิตศาสตร์อย่างไรให้ได้ดี

วิธีเรียนคณิตให้เก่ง เรียนคณิตศาสตร์อย่างไรให้ได้ดี

เชื่อว่าผู้เรียนหลายคนคงจะพบปัญหากับการเรียนวิชาคณิตศาสตร์ แล้วเราจะมีวิธีเรียนคณิตให้เก่ง เรียนคณิตศาสตร์อย่างไรให้ได้ดี วันนี้จะได้พบกับกลเม็ดเคล็ด (ไม่) ลับสำหรับการเรียนคณิตศาสตร์

เราต้องเริ่มฝึกฝนการเป็นผู้เรียนที่ดี โดยสามารถทำได้ตามขั้นตอนต่าง ๆ ดังนี้
1.  เวลาฟังครู หรือเวลาอ่าน ต้อง คิด ถาม จด ถ้าไม่เข้าใจควรจดคำถามไว้เพื่อคิดค้นคว้า หรือ ถามผู้รู้ต่อไป2.  หมั่นดูหนังสือหรือทำการบ้านอย่างมีประสิทธิภาพ ควรหามุมอ่านหรือทำการบ้านที่เหมาะสมกับตนเอง3.  จัดเวลาสำหรับทบทวนสิ่งที่เรียนมา หรืออ่านล่วงหน้าสิ่งที่จะเรียนต่อไป และถ้าปฏิบัติตามที่กำหนดได้ควรให้ รางวัลตัวเอง เช่น ได้ขนม ได้เล่น ได้ฟังเพลง ดูทีวี ได้เล่นกีฬา เป็นต้น ถ้า ทำไม่ได้ตาม กำหนดควรหาเวลาชดเชย4.  ทบทวนความรู้กับเพื่อน อย่าหวงวิชา แบ่งปันความรู้อธิบายให้กันและกัน อย่าช่วยเหลือเพื่อนในทางที่ผิด เช่น ทุจริตเวลาสอบ หรือให้ลอกงานโดยไม่เข้าใจ

5.  ศึกษาด้วยตนเอง มิใช่ต้องเรียนจากครูเพียงอย่างเดียว การศึกษาด้วยตนเองจากตำราหลายๆ เล่ม ต้องทำ ความเข้าใจจดสาระสำคัญต่าง ๆ ลงในโน้ตย่อ จดสิ่งที่ไม่เข้าใจไว้ค้นคว้าต่อไป ถ้าต้องการเชี่ยวชาญ คณิตศาสตร์ ต้องหมั่นหาโจทย์แปลกใหม่มาทำมาก ๆ เช่นโจทย์แข่งขัน เป็นต้น6. รู้ ๆ กันอยู่ว่า คณิตศาสตร์มีสูตร มีทฤษฎีมากมาย ทำอย่างไรถึงจะจำได้หมดล่ะ ? เราต้องเรียนด้วยความเข้าใจเสียก่อน จากนั้นเราต้องหมั่นทบทวน ก่อนอื่นเราจะต้องมีความรู้เกี่ยวกับ การจำการลืมก่อน 

ดังนั้น จึงสรุปได้ว่า เราควรทำความเข้าใจกับเรื่องนั้นๆเสียก่อน และหมั่นทบทวนทุกวันด้วย อ้อ อีกนิดหนึ่ง ถ้าอยากจำได้ดีและเข้าใจในเรื่องนั้นๆมากขึ้น เราควรที่จะ มองเปรียบเทียบคณิตเรื่องนั้นกับ เรื่องราวในชีวิตประจำวัน เช่น มองสิ่งต่างๆที่พบเจอเป็นคณิตศาสตร์ เป็นต้น

แล้วถ้า เกิดไม่ชอบวิชานี้เอามากๆ จะทำอย่างไรดีล่ะ ?

**สาเหตุที่ เรียนคณิตศาสตร์ได้ไม่ดีของหลาย ๆ คน มักมาจากการที่ไม่ชอบวิชานี้เอามากๆ ทำยังไงก็อ่านมันไม่เข้าใจ ทำใจให้ชอบมันไม่ได้เสียที มีหลักการง่ายๆที่ว่า ถ้าไม่ชอบมัน ก็เกลียดมันเสียเลยค่ะ คิดซะว่ามันเป็นคู่ต่อสู้ของเรา เราต้องเอาชนะมันให้ได้ อย่าไปยอมแพ้มัน ถ้าเกิดเรายอมแพ้แก่มัน…แล้วเราก็จะไม่มีวันชนะมันได้สักที ใช่ไหมล่ะค่ะ??
**สำหรับผู้ที่ไม่ชอบชอบวิชานี้ลองเปิดใจ เปลี่ยนทัศนคติใหม่ เปิดใจยอมรับ และมองในแง่ที่ดีกว่านี้ และก็ต้องขยันให้มาก ๆ 

การคูณ

การคูณ คือการดำเนินการทางคณิตศาสตร์อย่างหนึ่ง ทำให้เกิดการเพิ่มหรือลดจำนวนจำนวนหนึ่งเป็นอัตรา การคูณเป็นหนึ่งในสี่ของการดำเนินการพื้นฐานของเลขคณิตมูลฐาน (การดำเนินการอย่างอื่นได้แก่ การบวก การลบ และการหาร)

การคูณสามารถนิยามบนจำนวนธรรมชาติว่าเป็นการบวกที่ซ้ำๆ กัน ตัวอย่างเช่น 4 คูณด้วย 3 (หรือเรียกโดยย่อว่า 4 คูณ 3) หมายถึงการบวกจำนวน 4 เข้าไป 3 ชุด ดังนี้

สำหรับการคูณของจำนวนตรรกยะ (เศษส่วน) และจำนวนจริง ก็นิยามโดยกรณีทั่วไปที่เป็นระบบของแนวความคิดพื้นฐานดังกล่าว

การคูณอาจมองได้จากการนับวัตถุที่จัดเรียงกันเป็นรูปสี่เหลี่ยมผืนผ้า (สำหรับจำนวนธรรมชาติ) หรือการหาพื้นที่ของรูปสี่เหลี่ยมผืนผ้าโดยการหนดความยาวของด้านมาให้ (สำหรับจำนวนทั่วไป) ส่วนกลับของการคูณคือการหาร ในเมื่อ 4 คูณด้วย 3 เท่ากับ 12 ดังนั้น 12 หารด้วย 3 ก็จะเท่ากับ 4 เป็นต้น

เศษส่วน

ในทางคณิตศาสตร์ เศษส่วน คือความสัมพันธ์ตามสัดส่วนระหว่างชิ้นส่วนของวัตถุหนึ่งเมื่อเทียบกับวัตถุทั้งหมด เศษส่วนประกอบด้วยตัวเศษ(numerator) หมายถึงจำนวนชิ้นส่วนของวัตถุที่มี และตัวส่วน (denominator) หมายถึงจำนวนชิ้นส่วนทั้งหมดของวัตถุนั้น ตัวอย่างเช่น 34 อ่านว่า เศษสามส่วนสี่ หรือ สามในสี่ หมายความว่า วัตถุสามชิ้นส่วนจากวัตถุทั้งหมดที่แบ่งออกเป็นสี่ส่วนเท่าๆ กัน นอกจากนั้น การแบ่งวัตถุสิ่งหนึ่งออกเป็นศูนย์ส่วนเท่า ๆ กันนั้นเป็นไปไม่ได้ ดังนั้น 0 จึงไม่สามารถเป็นตัวส่วนของเศษส่วนได้ (ดูเพิ่มที่ การหารด้วยศูนย์)

เศษส่วนเป็นตัวอย่างชนิดหนึ่งของอัตราส่วน ซึ่งเศษส่วนแสดงความสัมพันธ์ระหว่างชิ้นส่วนย่อยต่อชิ้นส่วนทั้งหมด ในขณะที่อัตราส่วนพิจารณาจากปริมาณของสองวัตถุที่แตกต่างกัน (ดังนั้น 34 อาจไม่เท่ากับ 3 : 4) และเศษส่วนนั้นอาจเรียกได้ว่าเป็นผลหาร (quotient) ของจำนวน ซึ่งปริมาณที่แท้จริงสามารถคำนวณได้จากการหารตัวเศษด้วยตัวส่วน ตัวอย่างเช่น 34 คือการหารสามด้วยสี่ ได้ปริมาณเท่ากับ 0.75 ในทศนิยม หรือ 75% ในอัตราร้อยละ

การเขียนเศษส่วน ให้เขียนแยกออกจากกันด้วยเครื่องหมายทับหรือ ซอลิดัส (solidus) แล้ววางตัวเศษกับตัวส่วนในแนวเฉียง เช่น ¾ หรือคั่นด้วยเส้นแบ่งตามแนวนอนเรียกว่า วิงคิวลัม (vinculum) เช่น 34 ในบางกรณีอาจพบเศษส่วนที่ไม่มีเครื่องหมายคั่น อาทิ ³₄ บนป้ายจราจรในบางประเทศ

การบวก

การบวก คือกระบวนการทางคณิตศาสตร์โดยการรวมสิ่งของเข้าด้วยกัน เครื่องหมายบวก (+) ถูกใช้แทนความหมายของการบวกจำนวนหลายจำนวน จากตัวอย่างภาพทางขวา แอปเปิล 3 + 2 ผล หมายความว่ามีแอปเปิล 3 ผลกลุ่มหนึ่ง และมีแอปเปิล 2 ผลอีกกลุ่มหนึ่ง ซึ่ง 3 + 2 = 5 ดังนั้นจึงเหมือนกับว่ามีแอปเปิล 5 ผล นอกจากการนับจำนวนแล้ว การบวกสามารถนำเสนอได้โดยการรวมกลุ่มปริมาณทางรูปธรรมหรือนามธรรมอื่นๆ โดยใช้ประเภทที่แตกต่างกันของจำนวน เช่น จำนวนลบ เศษส่วน จำนวนตรรกยะ เวกเตอร์ ฯลฯ

ในฐานะของการดำเนินการทางคณิตศาสตร์ การบวกดำเนินตามแบบแผนที่สำคัญบางประการ เช่นการบวกมีสมบัติการสลับที่ หมายความว่าลำดับของการบวกนั้นไม่สำคัญ และการบวกมีสมบัติการเปลี่ยนหมู่ นั่นคือเราสามารถบวกกันได้มากกว่าสองจำนวน (ดูเพิ่มที่ ผลรวม) การบวกซ้ำๆ ด้วย 1 มีความหมายเหมือนการนับ ในขณะที่การบวกด้วย 0 จะไม่ทำให้จำนวนเปลี่ยนแปลง นอกจากนี้การบวกยังคล้อยตามกฎเกณฑ์ที่ทำนายได้ เกี่ยวกับการดำเนินการที่เกี่ยวข้องเช่นการลบและการคูณ กฎเกณฑ์ทั้งหมดเหล่านี้สามารถพิสูจน์ได้ โดยเริ่มต้นจากการบวกของจำนวนธรรมชาติ แล้วขยายขอบเขตออกไปยังจำนวนจริงและสูงขึ้นไป การดำเนินการทวิภาคทั่วไปที่คล้อยตามแบบแผนเหล่านี้ มีการศึกษาในพีชคณิตนามธรรม

การบวกเป็นหนึ่งในงานที่พื้นฐานที่สุดที่เกี่ยวข้องกับจำนวนตัวเลข การบวกของจำนวนน้อยๆ สามารถเรียนรู้ได้ตั้งแต่ยังเป็นเด็กเล็ก เด็กทารกอายุห้าเดือนรวมทั้งสัตว์บางชนิดก็สามารถรับรู้ว่า 1 + 1 จะได้ผลอะไร ในการเรียนระดับประถมศึกษา เด็กนักเรียนจะได้เรียนรู้การบวกจำนวนในระบบเลขฐานสิบ โดยเริ่มต้นจากจำนวนเลขหลักเดียว และพัฒนาการแก้ปัญหาในระดับที่ยากขึ้น เครื่องกลที่ช่วยคำนวณการบวกก็แตกต่างกันไปตั้งแต่ลูกคิดโบราณจนไปถึงคอมพิวเตอร์สมัยใหม่ ซึ่งการค้นคว้าวิจัยเกี่ยวกับการบวกที่มีประสิทธิภาพมากที่สุดยังคงดำเนินมาจนถึงทุกวันนี้

โครงสร้างระบบจำนวน

           จากรูปแผนผังข้างบนจะเห็นได้ว่า นอกจากจำนวนจริงแล้ว ยังมีจำนวนจินตภาพ ซึ่งเราจะไม่สนใจศึกษาในบทเรียนนี้ นอกจากนี้ เราจะเห็นได้ว่า จำนวนจริงประกอบด้วย จำนวนอตรรกยะ และ จำนวนตรรกยะ ซึ่งเราจะพิจารณาในรายละเอียดได้ดังนี้

• จำนวนอตรรกยะ  คือ จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือ ทศนิยมซ้ำได้ ยกตัวอย่างเช่น √2, √3, √5 หรือค่า ¶ เป็นต้น
• จำนวนตรรกยะ คือ จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือ ทศนิยมซ้ำได้ ยกตัวอย่างเช่น 1/2, 1/3, 2/5 เป็นต้น

จากแผนภาพอีกเช่นเคย จะเห็นได้ว่า จำนวนตรรกยะ จะประกอบด้วยสองส่วนคือ จำนวนเต็ม และจำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม

• จำนวนเต็ม คือจำนวนที่เป็นตัวเลขเต็มๆ หรือ ตัวเลขที่ไม่มีทศนิยมนั่นเอง นั่นคือ ตัวเลขที่เราใช้นับนั่นเอง ยกตัวอย่างเช่น 1, 2, 3, 4 ... ทั้งนี้ทั้งนั้น รวมไปจนถึงค่าที่ติบลบของจำนวนนับนี้และศูนย์ด้วย เช่น 0, -1, -2, -3, -4 ....
• จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม ความหมายของจำนวนนี้ก็ตามความหมายของชื่อเลยครับ นั่นคือ ตัวเลขเขียนในรูปของทศนิยมซ้ำได้โดยที่ไม่ได้เป็นเลขจำนวนเต็มนั่นเอง อย่างเช่น 1/2=0.5 หรือ 1/3 = 0.333... (สามซ้ำ)

ยิ่งไปกว่านั้น จำนวนเต็มยังแบ่งย่อยได้อีกสามหมวดคือ จำนวนเต็มลบ จำนวนเต็มบวก และ จำนวนเต็มศูนย์

การหาร

การหาร (อังกฤษ: division) ในทางคณิตศาสตร์ คือ การดำเนินการเลขคณิตที่เป็นการดำเนินการผันกลับของการคูณ และบางครั้งอาจมองได้ว่าเป็นการทำซ้ำการลบ พูดง่ายๆ คือการแบ่งออกหรือเอาเอาออกเท่าๆ กัน จนกระทั่งตัวหารเหลือศูนย์ (หารลงตัว)

ถ้า

a × b = c,

เมื่อ b ไม่เท่ากับ 0 แล้ว

a = c ÷ b

(อ่านว่า "c หารด้วย b") ตัวอย่างเช่น 6 ÷ 3 = 2 เพราะว่า 2 × 3 = 6

ในนิพจน์ข้างบน a คือ ผลหาร, b คือ ตัวหาร และ c คือ ตัวตั้งหาร

นิพจน์ c ÷ b มักเขียนแทนด้วย "c/b" โดยเฉพาะในคณิตศาสตร์ขั้นสูง (รวมถึงการประยุกต์ในวิทยาศาสตร์และวิศวกรรม) และในภาษาโปรแกรม การเขียนแบบนี้ มักใช้แทนเศษส่วน ซึ่งยังไม่ต้องการหาค่า

ในภาษาอื่นๆ ที่ไม่ใช่ภาษาอังกฤษ c ÷ b มักเขียนว่า c : b ซึ่งในภาษาอังกฤษ จะใช้เครื่องหมายทวิภาค (:) เมื่อมันเกี่ยวข้องกับสัดส่วน

สำหรับการหารด้วยศูนย์นั้น ไม่นิยาม

คณิตศาสตร์คือออะไร

ในอดีตผู้คนจะใช้สิ่งของแทนจำนวนที่จะนับยิ่งนานเข้าจำนวนประชากรยิ่งมีมากขึ้น ทำให้ผู้คนเริ่มคิดที่จะประดิษฐ์ตัวเลขขึ้นมาแทนการนับที่ใช้สิ่งของนับแทนจากนั้นก็มีการบวก ลบคูณ และหาร จากนั้นก็ก่อให้เกิดคณิตศาสตร์ คณิตศาสตร์ เป็นศาสตร์ที่มุ่งค้นคว้าเกี่ยวกับ โครงสร้างนามธรรมที่ถูกกำหนดขึ้นผ่านทางกลุ่มของสัจพจน์ซึ่งมีการให้เหตุผลที่แน่นอนโดยใช้ตรรกศาสตร์สัญลักษณ์ และสัญกรณ์คณิตศาสตร์ เรามักนิยามโดยทั่วไปว่าคณิตศาสตร์เป็นสาขาวิชาที่ศึกษาเกี่ยวกับรูปแบบและโครงสร้าง, การเปลี่ยนแปลง, และปริภูมิ กล่าวคร่าวๆ ได้ว่าคณิตศาสตร์นั้นสนใจ "รูปร่างและจำนวน" เนื่องจากคณิตศาสตร์มิได้สร้างความรู้ผ่านกระบวนการทดลอง บางคนจึงไม่จัดว่าคณิตศาสตร์เป็นสาขาของวิทยาศาสตร์

คำว่า "คณิตศาสตร์" (คำอ่าน: คะ-นิด-ตะ-สาด) มาจากคำว่า คณิต (การนับ หรือ คำนวณ) และ ศาสตร์ (ความรู้ หรือ การศึกษา) ซึ่งรวมกันมีความหมายโดยทั่วไปว่า การศึกษาเกี่ยวกับการคำนวณ หรือ วิชาที่เกี่ยวกับการคำนวณ. คำนี้ตรงกับคำภาษาอังกฤษว่า mathematics มาจากคำภาษากรีก μάθημα (máthema) แปลว่า "วิทยาศาสตร์, ความรู้, และการเรียน" และคำว่า μαθηματικός (mathematikós) แปลว่า "รักที่จะเรียนรู้". ในอเมริกาเหนือนิยมย่อ mathematics ว่า math ส่วนประเทศอื่นๆ ที่ใช้ภาษาอังกฤษนิยมย่อว่า maths

ความรู้ทางด้านคณิตศาสตร์เพิ่มขึ้นอย่างสม่ำเสมอ ผ่านทางการวิจัยและการประยุกต์ใช้ คณิตศาสตร์เป็นเครื่องมืออันหนึ่งของวิทยาศาสตร์ อย่างไรก็ตาม การคิดค้นทางคณิตศาสตร์ไม่จำเป็นต้องมีเป้าหมายอยู่ที่การนำไปใช้ทางวิทยาศาสตร์ (ดู คณิตศาสตร์บริสุทธิ์ และคณิตศาสตร์ประยุกต์)

โครงสร้างต่างๆ ที่นักคณิตศาสตร์สนใจและพิจารณานั้น มักจะมีต้นกำเนิดจากวิทยาศาสตร์ธรรมชาติ และสังคมศาสตร์ โดยเฉพาะฟิสิกส์ และเศรษฐศาสตร์. ปัญหาทางคณิตศาสตร์ในปัจจุบัน ยังเกี่ยวข้องกับการประยุกต์ใช้ในสาขาวิทยาการคอมพิวเตอร์ และทฤษฎีการสื่อสาร อีกด้วย

เนื่องจากคณิตศาสตร์นั้นใช้ตรรกศาสตร์สัญลักษณ์และสัญกรณ์คณิตศาสตร์ ซึ่งทำให้กิจกรรมทุกอย่างกระทำผ่านทางขั้นตอนที่ชัดเจน เราจึงสามารถพิจารณาคณิตศาสตร์ว่า เป็นระบบภาษาที่เพิ่มความแม่นยำและชัดเจนให้กับภาษาธรรมชาติ ผ่านทางศัพท์และไวยากรณ์บางอย่าง สำหรับการอธิบายและศึกษาความสัมพันธ์ทั้งทางกายภาพและนามธรรม. ความหมายของคณิตศาสตร์นั้นยังมีอีกหลายมุมมอง ซึ่งหลายอันถูกกล่าวถึงในบทความเกี่ยวกับปรัชญาของคณิตศาสตร์

คณิตศาสตร์ยังถูกจัดว่าเป็นศาสตร์สัมบูรณ์ โดยจำไม่เป็นต้องมีการอ้างถึงใดๆ จากโลกภายนอก. นักคณิตศาสตร์กำหนดและพิจารณาโครงสร้างบางประเภท สำหรับใช้ในคณิตศาสตร์เองโดยเฉพาะ, เนื่องจากโครงสร้างเหล่านี้ อาจทำให้สามารถอธิบายสาขาย่อยๆ หลายๆ สาขาได้ในภาพรวม หรือเป็นประโยชน์ในการคำนวณพื้นฐาน

นอกจากนี้ นักคณิตศาสตร์หลายคนก็ทำงานเพื่อเป้าหมายเชิงสุนทรียภาพเท่านั้น โดยมองว่าคณิตศาสตร์เป็นศาสตร์เชิงศิลปะ มากกว่าที่จะเป็นศาสตร์เพื่อการนำไปประยุกต์ใช้ (ดังเช่น จี. เอช. ฮาร์ดี ที่ได้กล่าวไว้ในหนังสือ A Mathematician's Apology) ; แรงผลักดันในการทำงานเช่นนี้ มีลักษณะไม่ต่างไปจากที่กวีและนักปรัชญาได้ประสบ และเป็นสิ่งที่ไม่สามารถอธิบายได้. อัลเบิร์ต ไอน์สไตน์ กล่าวว่า คณิตศาสตร์เป็นราชินีของวิทยาศาสตร์ ในหนังสือ Ideas and Opinions ของเขา

องค์ความรู้ในคณิตศาสตร์รวมกันเป็นสาขาวิชา หลักการเบื้องต้นที่เริ่มจากเลขคณิตไปยังการประยุกต์ใช้งานพื้นฐานของสาขาคณิตศาสตร์ ที่รวมพีชคณิต เรขาคณิต ตรีโกณมิติ สถิติศาสตร์ และแคลคูลัส เป็นหลักสูตรแกนในการศึกษาขั้นพื้นฐาน แม้ว่าจะได้มีการพัฒนาและขยายขอบเขตไปอย่างมากมายในช่วงเวลาหลายร้อยปี สาขาวิชาคณิตศาสตร์ยังคงถูกจัดว่าเป็นสาขาวิชาเดี่ยว ที่มีลักษณะแตกต่างจากสาขาอื่นๆ